Метод Гаусса для чайников: примеры решений. Метод Гаусса: описание алгоритма решения системы линейных уравнений, примеры, решения

Раздел 3. Численные методы решения уравнений

Виды математических моделей (уравнений) в теории электрических цепей

1. - системы линейных алгебраических уравнений –

линейные цепи постоянного и синусоидального переменного (комплексный метод) тока.

2 . - системы нелинейных алгебраических или

трансцендентных уравнений – нелинейные цепи постоянного или синусоидального тока.

3. . – системы нелинейных дифференциальных

уравнений первого порядка в обыкновенных производных – переходные процессы в нелинейных цепях.

Здесь F и ψ – вектор-функции, т.е. эквивалентно записи:

f 1 (X,b 1) = 0

f 2 (X,b 2) = 0

…………

f n (X,b n) = 0

а - записи:

ψ 1 (dX/dt,X,b 1 ,t) = 0

ψ 2 (dX/dt,X,b 2 ,t) = 0

…………………..

ψ n (dX/dt,X,b n ,t) = 0

Рассмотрим наиболее эффективные методы решения этих уравнений.

Численные методы решения систем линейных алгебраических уравнений (ЛАУ)

Метод Гаусса (исключения неизвестных)

Методы решения ЛАУ имеют важное значение, так как они применяются (итерационно) для решения более сложных уравнений.

Пусть система ЛАУ задана в виде:

,

где - квадратная матрица n – го порядка с ненулевыми диагональными элементами ; - вектор неизвестных; - вектор правых частей.

Алгоритм метода Гаусса состоит из прямого и обратного хода. Во время прямого хода осуществляется последовательное исключение неизвестных. Система приобретает вид:

Пересчет коэффициентов производится по формуле:

, где i, j = k+1, …n при исключение k -го неизвестного.

При этом столбец правых частей удобно рассматривать как n + 1 столбец матрицы коэффициентов , т.е. j = k+1, …n+1.

Обратный ход заключается в определении неизвестных, начиная с последнего уравнения где осталась одна неизвестная x n . Полученное значение x n подставляется в предыдущее уравнение и определяется x n -1 и т.д.

Для произвольного x k получается следующая формула:

где k = n, n -1,…1.

Трудоемкость метода Гаусса оценивается количеством выполняемых арифметических операций:

.

Кубическая зависимость от размерности задачи существенно ограничивает сложность анализируемых цепей. Однако если часть коэффициентов a ik в матрице равна нулю, т.е. она является разреженной , то появляется возможность сокращения трудоемкости.

Основная идея метода разреженных матриц состоит в учете при вычислениях и хранении только ненулевых элементов матрицы . Степень разреженности матрицы характеризуется коэффициентом заполнения:

где n ннэ –число ненулевых элементов.

Существуют матрицы коэффициентов специального вида: ленточные, когда ненулевые элементы располагаются вдоль главной диагонали; и блочно-диагональные, когда вдоль главной диагонали располагаются ненулевые блоки. Еще встречаются блочно-диагональные с окаймлением.

Пример ленточной матрицы Пример блочно-диагональной матрицы

Пример блочно-диагональной матрицы с окаймлением

Для них разработаны специальные эффективные методы решения. Для диагональной – метод прогонки . Блочная распадается на отдельные группы уравнений по блокам, которые решаются методом Гаусса. Для блочно-диагональных с окаймлением существуют диакоптические методы решения.

Диакоптика – подход к исследованию сложных систем, заключающейся в расчленение системы на части и её анализе по частям при учете всех связей между выделенными частями.

Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса, далее - просто прямой ход). Пример такой системы и её решения - на рисунке сверху.

В такой системе последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение (обратный ход метода Гаусса , далее - просто обратный ход), из которого находят предыдущую переменную, и так далее.

В трапециевидной (треугольной) системе, как видим, третье уравнение уже не содержит переменных y и x , а второе уравнение - переменной x .

После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.

Преимущества метода:

1. при решении систем линейных уравнений с числом уравнений и неизвестных более трёх метод Гаусса не такой громоздкий, как метод Крамера , поскольку при решении методом Гаусса необходимо меньше вычислений;
2. методом Гаусса можно решать неопределённые системы линейных уравнений, то есть, имеющие общее решение (и мы разберём их на этом уроке), а, используя метод Крамера, можно лишь констатировать, что система неопределённа;
3. можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений (также разберём их на этом уроке);
4. метод основан на элементарных (школьных) методах - методе подстановки неизвестных и методе сложения уравнений, которых мы коснулись в соответствующей статье.

Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.

Пример 1. Решить систему линейных уравнений, применяя обратный ход:

Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y :

Теперь нам известны значения уже двух переменных - z и y . Подставляем их в первое уравнение и получаем значение переменной x :

Из предыдущих шагов выписываем решение системы уравнений:

Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.

Элементарные преобразования системы линейных уравнений

Повторяя школьный метод алгебраического сложения уравнений системы, мы выяснили, что к одному из уравнений системы можно прибавлять другое уравнение системы, причём каждое из уравнений может быть умножено на некоторые числа. В результате получаем систему линейных уравнений, эквивалентную данной. В ней уже одно уравнение содержало только одну переменную, подставляя значение которой в другие уравнений, мы приходим к решению. Такое сложение - один из видов элементарного преобразования системы. При использовании метода Гаусса можем пользоваться несколькими видами преобразований.

На анимации выше показано, как система уравнений постепенно превращается в трапециевидную. То есть такую, которую вы видели на самой первой анимации и сами убедились в том, что из неё просто найти значения всех неизвестных. О том, как выполнить такое превращение и, конечно, примеры, пойдёт речь далее.

При решении систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно :

1. переставлять местами строки (это и было упомянуто в самом начале этой статьи);
2. если в результате других преобразований появились равные или пропорциональные строки, их можно удалить, кроме одной;
3. удалять "нулевые" строки, где все коэффициенты равны нулю;
4. любую строку умножать или делить на некоторое число;
5. к любой строке прибавлять другую строку, умноженное на некоторое число.

В результате преобразований получаем систему линейных уравнений, эквивалентную данной.

Алгоритм и примеры решения методом Гаусса системы линейных уравнений с квадратной матрицей системы

Рассмотрим сначала решение систем линейных уравений, в которых число неизвестных равно числу уравнений. Матрица такой системы - квадратная, то есть в ней число строк равно числу столбцов.

Пример 2. Решить методом Гаусса систему линейных уравнений

Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.

Для упрощения внешнего вида решения составим расширенную матрицу системы :

В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты - свободные члены.

Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы . Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:

С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений . Для этого ко второй строке матрицы прибавим первую строку, умноженную на (в нашем случае на ), к третьей строке – первую строку, умноженную на (в нашем случае на ).

Это возможно, так как

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x :

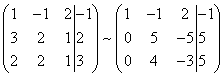
Для упрощения второй строки полученной системы умножим её на и получим вновь матрицу системы уравнений, эквивалентной данной системе:

Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на (в нашем случае на ).

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:

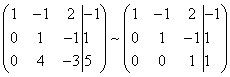
Мы получили эквивалентную данной трапециевидную систему линейных уравнений:

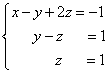
Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в нашем демо-примере.

Решение найдём "с конца" - обратный ход . Для этого из последнего уравнения определим z :
.
Подставив это значение в предшествующее уравнение, найдём y :

Из первого уравнения найдём x :

Ответ: решение данной системы уравнений - .

: в этом случае будет выдан тот же ответ, если система имеет однозначное решение. Если же система имеет бесконечное множество решений, то таков будет и ответ, и это уже предмет пятой части этого урока.

Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение

Перед нами вновь пример совместной и определённой системы линейных уравнений, в которой число уравнений равно числу неизвестных. Отличие от нашего демо-примера из алгоритма - здесь уже четыре уравнения и четыре неизвестных.

Пример 4. Решить систему линейных уравнений методом Гаусса:

Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Проведём подготовительные работы. Чтобы было удобнее с отношением коэффициентов, нужно получить единицу в во втором столбце второй строки. Для этого из второй строки вычтем третью, а полученную в результате вторую строку умножим на -1.

Проведём теперь собственно исключение переменной из третьего и четвёртого уравнений. Для этого к третьей строке прибавим вторую, умноженную на , а к четвёртой - вторую, умноженную на .

Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на . Получаем расширенную матрицу трапециевидной формы.

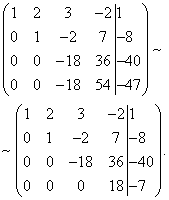
Получили систему уравнений, которой эквивалентна заданная система:

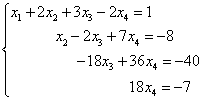
Следовательно, полученная и данная системы являются совместными и определёнными. Окончательное решение находим «с конца». Из четвёртого уравнения непосредственно можем выразить значение переменной "икс четвёртое":

Это значение подставляем в третье уравнение системы и получаем

,

,

Наконец, подстановка значений

В первое уравнение даёт

,

откуда находим "икс первое":

Ответ: данная система уравнений имеет единственное решение .

Проверить решение системы можно и на калькуляторе, решающем методом Крамера : в этом случае будет выдан тот же ответ, если система имеет однозначное решение.

Решение методом Гаусса прикладных задач на примере задачи на сплавы

Системы линейных уравнений применяются для моделирования реальных объектов физического мира. Решим одну из таких задач - на сплавы. Аналогичные задачи - задачи на смеси, стоимость или удельный вес отдельных товаров в группе товаров и тому подобные.

Пример 5. Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй - 30%, третий - 10%. При этом во втором и третьем сплавах вместе взятых меди на 28,4 кг меньше, чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.

Решение. Составляем систему линейных уравнений:

Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений:

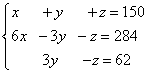
Составляем расширенную матрицу системы:

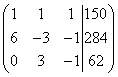
Внимание, прямой ход. Путём сложения (в нашем случае - вычитания) одной строки, умноженной на число (применяем два раза) с расширенной матрицей системы происходят следующие преобразования:

Прямой ход завершился. Получили расширенную матрицу трапециевидной формы.

Применяем обратный ход. Находим решение с конца. Видим, что .

Из второго уравнения находим

Из третьего уравнения -

Проверить решение системы можно и на калькуляторе, решающем методом Крамера : в этом случае будет выдан то же ответ, если система имеет однозначное решение.

О простоте метода Гаусса говорит хотя бы тот факт, что немецкому математику Карлу Фридриху Гауссу на его изобретение потребовалось лишь 15 минут. Кроме метода его имени из творчества Гаусса известно изречение "Не следует смешивать то, что нам кажется невероятным и неестественным, с абсолютно невозможным" - своего рода краткая инструкция по совершению открытий.

Во многих прикладных задачах может и не быть третьего ограничения, то есть, третьего уравнения, тогда приходится решать методом Гаусса систему двух уравнений с тремя неизвестными, или же, наоборот - неизвестных меньше, чем уравнений. К решению таких систем уравнений мы сейчас и приступим.

С помощью метода Гаусса можно установить, совместна или несовместна любая система n линейных уравнений с n переменными.

Метод Гаусса и системы линейных уравнений, имеющие бесконечное множество решений

Следующий пример - совместная, но неопределённая система линейных уравнений, то есть имеющая бесконечное множество решений.

После выполнения преобразований в расширенной матрице системы (перестановки строк, умножения и деления строк на некоторое число, прибавлению к одной строке другой) могли появиться строки вида

Если во всех уравнениях имеющих вид

Свободные члены равны нулю, то это означает, что система неопределённа, то есть имеет бесконечное множество решений, а уравнения этого вида – «лишние» и их исключаем из системы.

Пример 6.

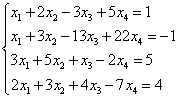
Решение. Составим расширенную матрицу системы. Затем с помощью первого уравнения исключим переменную из последующих уравнений. Для этого ко второй, третьей и четвёртой строкам прибавим первую, умноженную соответственно на :

Теперь вторую строку прибавим к третьей и четвёртой.

В результате приходим к системе

Последние два уравнения превратились в уравнения вида . Эти уравнения удовлетворяются при любых значениях неизвестных и их можно отбросить.

Чтобы удовлетворить второму уравнению, мы можем для и выбрать произвольные значения , тогда значение для определится уже однозначно: . Из первого уравнения значение для также находится однозначно: .

Как заданная, так и последняя системы совместны, но неопределённы, и формулы

при произвольных и дают нам все решения заданной системы.

Метод Гаусса и системы линейных уравнений, не имеющие решений

Следующий пример - несовместная система линейных уравнений, то есть не имеющая решений. Ответ на такие задачи так и формулируется: система не имеет решений.

Как уже говорилось в связи с первым примером, после выполнения преобразований в расширенной матрице системы могли появиться строки вида

соответствующие уравнению вида

Если среди них есть хотя бы одно уравнение с отличным от нуля свободным членом (т.е. ), то данная система уравнений является несовместной, то есть не имеет решений и на этом её решение закончено.

Пример 7. Решить методом Гаусса систему линейных уравнений:

Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную . Для этого ко второй строке прибавляем первую, умноженную на , к третьей строке - первую, умноженную на , к четвёртой - первую, умноженную на .

Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Чтобы получить целые отношения коэффициентов, поменяем местами вторую и третью строки расширенной матрицы системы.

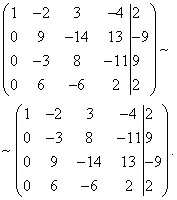
Для исключения из третьего и четвёртого уравнения к третьей строке прибавим вторую, умноженную на , а к четвёртой - вторую, умноженную на .

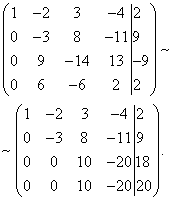
Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на .

Заданная система эквивалентна, таким образом, следующей:

Полученная система несовместна, так как её последнее уравнение не может быть удовлетворено никакими значениями неизвестных. Следовательно, данная система не имеет решений.

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку "Вычислить."

x 1 +x 2 +x 3 x 1 +x 2 +x 3 x 1 +x 2 +x 3 = = =

Представление чисел:

Целые числа и (или) Обыкновенные дроби
Целые числа и (или) Десятичные дроби

Число знаков после десятичного разделителя

×

Предупреждение

Очистить все ячейки?

Закрыть Очистить

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

• перемена местами двух уравнений в системе,
• умножение какого-либо уравнения в системе на ненулевое действительное число,
• прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

(1)

Запишем систему (1) в матричном виде:

Ax=b

(2)

(3)

A -называется матрица коэффициентов системы, b − правая часть ограничений, x − вектор переменных, которую нужно найти. Пусть rang(A )=p .

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a 22 . Для этого сложим строки 3, ... m со строкой 2, умноженной на −a 32 /a 22 , ..., −a m2 /a 22 , соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(7)

Так как rangA=rang (A|b ), то множество решений (7) есть (n−p )− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Обозначим через a ij элементы i -ой строки и j -ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a 1 1 . Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Подставив верхние выражения в нижние, получим решение.

Пусть дана система линейных уравнений

Коэффициенты при неизвестных составляют прямоугольную лицу

называемую матрицей системы. Первый индекс у коэффициента aij означает номер уравнения, второй - номер неизвестного, при котором стоит этот коэффициент. Коэффициенты Ь, , Ь гп называются свободными членами уравнений системы. Если свободные члены равны нулю, то система называется однородной , в противном случае - неоднородной. Матрицу

называют расширенной матрицей системы (2.1).

Решение системы (2.1) - это любой упорядоченный набор (ад, Х 2 , ? ??,х п) из п чисел, при подстановке которых в уравнения системы вместо соответствующих неизвестных каждое уравнение системы превращается в тождество. Система, не имеющая ни одного решения, называется несовместной , или противоречивой. Система, имеющая хотя бы одно решение, называется совместной.

Совместные системы подразделяют на определенные, обладающие единственным решением, и неопределенные, обладающие большим числом решений. Однородная система всегда совместна, так как имеет по крайней мере нулевое решение х - Х 2 - ... = х п = 0.

Выражения (формулы), содержащие неизвестные х, х 2, ..., х п и некоторый набор произвольных постоянных, из которых при соответствующем выборе значений произвольных постоянных можно получить любое конкретное решение системы, называют общим решением системы, а любое конкретное решение системы - ее частным решением. Две системы с одними и теми же неизвестными эквивалентны (равносильны ), если каждое решение одной из них является решением другой или обе системы несовместны.

Над уравнениями системы обычно приходится проводить следующие элементарные преобразования:

• 1) умножение обеих частей какого-либо уравнения на число, отличное от нуля;
• 2) прибавление (вычитание) к одному уравнению другого, умноженного на некоторое число;
• 3) перестановку уравнений;
• 4) вычеркивание уравнений вида 0 х + 0 Х 2 + + 0 х п = 0, т.е. тождеств 0 = 0;
• 5) перестановку неизвестных в системе уравнений.

В результате элементарных преобразований система преобразуется в эквивалентную. Общий способ отыскания решений обычно основывается на последовательном переходе с помощью элементарных преобразований от данной системы к такой эквивалентной системе, для которой решение находится просто. Одним из таких способов является метод последовательного исключения неизвестных (метод Гаусса). Алгоритм этого метода состоит в следующем.

Предположим, что коэффициент ац системы (2.1) отличен от нуля. Этого всегда можно добиться, переставляя в случае необходимости уравнения системы или неизвестные в ней и меняя нумерацию неизвестных. Умножим первое уравнение на а 2 /ац и вычтем из второго уравнения, затем на а^/ац и вычтем из третьего уравнения и т.д. Наконец, умножим первое уравнение на a m ja и вычтем из последнего уравнения. В результате неизвестное х будет исключено из всех уравнений, кроме первого, и система примет вид:

В системе (2.2) следует вычеркнуть уравнения вида 0 х + 0 Х 2 + ...+ +0 х п = 0, если такие появились. На этом первый шаг метода Гаусса заканчивается. Элемент Дц называют ведущим элементом этого шага.

Следующие шаги прямого хода метода Гаусса осуществляются аналогично. Так, на втором шаге при а 22 ^ 0 последовательно умножаем второе уравнение на а" 32 /а 22 , а! А2 /а! 22 , ..., a" m2 fa 22 и вычитаем его из 3-го, 4-го, ..., m-го уравнений. В результате неизвестное Х 2 исключается из всех уравнений, кроме 1-го и 2-го. На третьем шаге неизвестное хз исключается из всех уравнений, кроме первых трех, и т.д.

Возможно, что на некотором шаге прямого хода метода Гаусса встретится уравнение вида

Тогда рассматриваемая система несовместна, и дальнейшее ее решение прекращается. Если же при выполнении прямого хода метода Гаусса не встретятся уравнения вида (2.3), то рассматриваемая система не более чем через m шагов прямого хода преобразуется в эквивалентную систему вида

Для упрощения записи в системе (2.4) штрихи над коэффициентами опущены. В ней не более т уравнений, т.е. г ^ т, так как некоторые уравнения, возможно, были приведены к виду 0 = 0 и вычеркнуты, и, очевидно также, что г ^ п.

При г = п система (2.4) имеет треугольный вид:

и в ней легко совершить обратный ход метода Гаусса. Для этого из последнего уравнения этой системы найдем значение неизвестного х п. Подставив его в предпоследнее уравнение, найдем значение.x n _i. Продолжая так далее, однозначно определим все неизвестные х, Х 2 , ..., х п. Следовательно, если система (2.1) при прямом ходе метода Гаусса сводится к системе треугольного вида, то такая система определенная, т.е. имеет единственное решение.

При г система (2.4) имеет вид трапеции. В ней неизвестные х, Х 2 , ..., х г принимают за главные, а неизвестные х+, х г+ 2 , ..., х п - за свободные. Свободные неизвестные могут принимать любые фиксированные значения. Полагая x r+ = 7 r +i, х г+ 2 = Ъ-+ 2 , , х п = 7 п, где 7r+i, 7г+2? , 7п - произвольные постоянные, и проведя в системе обратный ход метода Гаусса, получим формулы:

которые составляют общее решение системы (2.1). Из общего решения (2.С) при конкретных значениях 7 r +i, 7г+2, , 7п будут получаться частные решения системы (2.1). Так как каждое свободное неизвестное может принимать бесчисленное множество значений, система (2.1) при г т.е. в случае, когда она приводится к трапецеидальному виду, обладает бесчисленным множеством решений. Это справедливо для совместных систем, имеющих меньше уравнений, чем неизвестных, и, в частности, для однородных, имеющих меньше уравнений, чем неизвестных.

На практике метод Гаусса обычно реализуют в матричной форме. Для этого выписывают расширенную матрицу системы, в которой для удобства отделяют вертикальной чертой столбец свободных членов, и преобразования проводят над этой матрицей, затем над полученной и т.д. При этом матрицы эквивалентных систем также считают эквивалентными.

Пример 2.1. Методом Гаусса решить систему уравнений

Решение. Оставляя в расширенной матрице системы

первую строку без изменения и вычитая утроенную первую строку из второй, удвоенную первую строку из третьей и четвертой, придем к эквивалентной матрице

Вычитая в этой матрице вторую строку из третьей и оставляя другие строки без изменения, получим матрицу

Вычеркивая здесь третью строку, придем к матрице

которая соответствует системе

Отсюда, совершая обратный ход метода Гаусса, найдем

При мер 2.2. Методом Гаусса решить систему уравнений

Решение. Если в расширенной матрице системы

первую строку оставить без изменения, удвоенную первую строку вычесть из второй, утроенную первую строку вычесть из третьей, то получим матрицу

Строка (0 0 0 | - 5) соответствует уравнению 0 х + 0 х 2 + 0 хз = -5. Наличие такого уравнения указывает на несовместность рассматриваемой системы. ?

Пример 2.3. Методом Гаусса решить систему уравнений

Решение. Элементарные преобразования прямого хода метода Гаусса над строками расширенной матрицы системы дают следующую цепочку эквивалентных матриц:

Последняя матрица этой цепочки соответствует системе

Полагая здесь хз = 73 (77 - произвольная постоянная) и проводя обратный ход метода Гаусса, получим общее решение:

Для повышения эффективности и устойчивости метода Гаусса его модифицируют различными способами. Например, часто применяют схему, в которой на каждом шаге прямого хода ведущий коэффициент выбирают наибольшим по модулю среди коэффициентов при неизвестных в выбранном уравнении или в подсистеме, с которой работают на данном этапе.

При решении систем "вручную" методом Гаусса, чтобы избежать сложных вычислений, иногда в промежутках между шагами прямого хода метода Гаусса или до его начала целесообразно проделывать дополнительные элементарные преобразования над некоторыми уравнениями системы. Например, при решении "вручную" системы

целесообразно сначала из первого уравнения системы вычесть удвоенное третье, а остальные оставить без изменения. Тогда получим систему

в которой метод Гаусса проводится уже легко. Дополнительные преобразования совершаются также над матрицами.

В заключение отметим, что метод Гаусса и его модификации находят самое широкое применение в вычислительной практике. Для его реализации на ЭВМ можно использовать стандартные программы, которые включены практически в любой пакет программ для решения математических задач.

Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное – просто! Кстати, портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Про миноры и алгебраические дополнения можно на время забыть! Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах.

Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и мы постараемся в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.

2) Иметь бесконечно много решений.

3) Не иметь решений (быть несовместной ).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы вновь рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№ 2-3 отведена статья Несовместные системы и системы с общим решением. Заметим, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе

И решим ее методом Гаусса.

На первом этапе запишем так называемую расширенную матрицу системы :

По какому принципу записаны коэффициенты, думаем, всем видно.

Примечание: Расширенная матрица системы получается из исходной с помощью «операции наращивания строк / столбцов». В данном случае матрицу нарастили за счёт столбца свободных членов исходной системы уравнений.

Примечание: Кроме перечисленных ранее 6-и алгебраических операций с матрицами и «операции наращивания» существует ещё «операция отбрасывания строк/столбцов». С помощью «операции отбрасывания строк/столбцов» составляют, например, подматрицы, определители которых являются минорами элементов матрицы.

Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто линия отчёркивания для удобства оформления.

Определение: Матрица системы – это матрица, составленная только из коэффициентов при неизвестных переменных системы линейных уравнений.

Определение: Расширенная матрица системы – это матрица системы, которую нарастили справа на столбец свободных членов.

В данном примере . – это матрица системы, а - это расширенная матрица системы. Любую из них можно для краткости называть просто матрицей.

После того, как записана расширенная матрица системы, с ней необходимо выполнить некоторые новые алгебраические действия, которые с лёгкой руки Гаусса называются также элементарными преобразованиями матрицы . Преобразования называют элементарными , потому что показано (будем считать это определением), что

Определение: После каждого элементарного преобразования расширенной матрицы получается совершенно другая матрица, но решения для этой новой системы линейных уравнений остаются теми же, что и для исходной матрицы .

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.

Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них:

.

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить . Рисовать не будем, понятно, нулевая строка – это строка, в которой одни нули .

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля.

Рассмотрим нашу матрицу из практического примера: . Сначала распишем преобразование очень подробно.

Умножаем первую строку на (-2): , далее ко второй строке прибавляем первую строку, оставляя первую без изменений : . Теперь первую строку можно разделить «обратно» на (–2): .

Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .

На практике так подробно, конечно, не расписывают, а пишут короче:

Еще раз: ко второй строке прибавили первую строку, умноженную на (–2) . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0.

Записываю результат во вторую строку: »

«Теперь второй столбец. Вверху –1 умножаю на –2: (-1∙(-2) = 2 ). Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку:

»

«И третий столбец. Вверху –5 умножаю на –2: (-5∙(-2) = 10 ). Ко второй строке прибавляю первую: (–7 + 10 = 3 ). Записываю результат во вторую строку:

»

Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Повторим: «Элементарные преобразования не изменяют решение системы»

ВНИМАНИЕ!: рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!

Вернемся к нашей системе . Она уже почти решена.

Что просит Гаусс? Он говорит: «Запишите расширенную матрицу системы и с помощью элементарных преобразований приведите ее к ступенчатому виду ».

В данном случае для этого

(1) Ко второй строке прибавьте первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Разделите вторую строку на 3. Почему? Чтобы вторая строка давала сразу значение второй переменной.

Цель элементарных преобразований – привести матрицу к ступенчатому виду:

В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .

В результате элементарных преобразований получена система уравнений, эквивалентная исходной системе линейных уравнений, которая приняла вид:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .

В нижнем уравнении у нас уже готовый результат: . Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Ответ:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас мы сразу нарисуем результат, к которому мы придём в ходе решения:

.

Повторимся, что наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:

.

Почти всегда здесь должна находиться единица . Вообще говоря, устроит и (–1), а иногда и другие числа, но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения . Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18).

И последовательно проводим (опять же мысленно или на черновике) сложение, т. е. ко второй строке прибавляем первую строку, уже умноженную на –2 :

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 .

Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО :

.

А мысленный ход самих расчётов мы уже рассмотрели выше.

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на (–2) и проведите сложение. Последнее выполненное действие – причёска результата, для этого делим третью строку на 3.

В результате элементарных преобразований получена система, эквивалентная исходной системе линейных уравнений:

Теперь в действие вступает «обратный ход» метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

Пример 3

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами.

Поступим так:

(1) К первой строке прибавляем вторую строку, умноженную на (–1) . То есть, мысленно умножили вторую строку на (–1) и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху (–1), что нас вполне устроит. Кто хочет получить (+1), может выполнить дополнительное телодвижение: умножить первую строку на (–1), сменив у неё знак. Дальше алгоритм работает уже по накатанной колее:

.

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на (–1). В принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:

Ответ: .

Пример 4

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваш ход решения может отличаться от нашего хода решения.

Предыдущая статья: Как выучить предмет за ночь перед экзаменом Следующая статья: Заготовка голубики